这里结合AlphaGo进行讲解

基础定义

1.动作空间
$\text{A}=\{1,\ldots,361\}$

2.状态定义
AlphaGoZero使用$19\times19\times17$表示一个状态
第三维中分为最近8步的黑子和白子，还有一维表示黑棋还是白棋

3.策略网络$\pi(a|s;\theta)$
通过softmax输出361维的动作概率分布

4.价值网络$v(s;\omega)$
这是对状态价值函数$V_{\pi}$的近似

策略网络和价值网络通过同一个卷积网络生成特征向量，然后分别用全连接网络得到最后结果

MCTS

MCTS的步骤: 选择，扩展，求值，回溯。这是一轮模拟的过程

第一步: 选择

从诸多动作中找几个好的动作进行搜索和评估

分值: $score(a)\overset{\triangle}{=}Q(a) + \frac{\eta}{1+N(a)}\cdot \pi(a|s;\theta)$
$\eta$是超参数
$N(a)$是动作a选中的次数，选中就执行加1操作
$Q(a)$初始值为0，并且不断更新的，更新的方式在第四步会说到

公式理解: $\frac{1}{1+N(a)}$鼓励探索，让选中次数少的更容易被选中
alt text
第三个动作分数最高，在这一轮的模拟中执行这个动作（不是真正下这步棋）

第二步: 扩展

猜测对手执行的动作
用之前训练好的策略网络模拟，随机抽样一个动作$a’_{t}\sim \pi(\cdot|s’_{t};\theta)$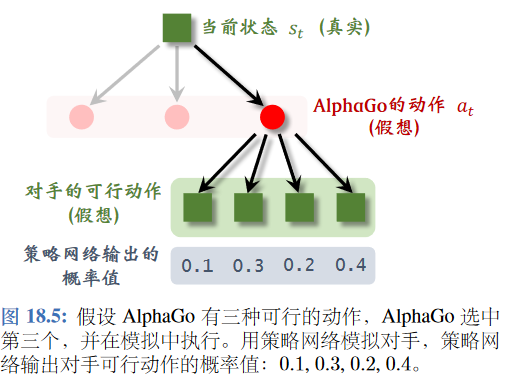
alt text
状态转移函数—>策略网络
注意我们的$s_{t+1}$不是AlphaGo执行完动作后的棋盘状态，而是在假想对手执行完以后得到的大小，如图所示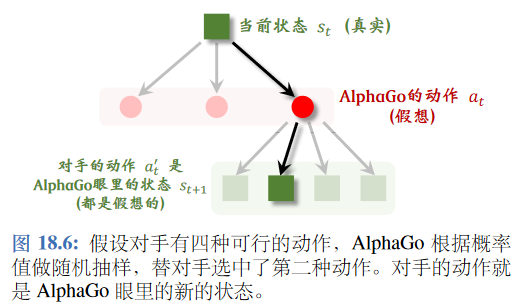
alt text

第三步: 求值

从状态$s_{t+1}$开始，双方都用策略网络$\pi$做决策，AlphaGo基于状态$s_k$，而对手基于对手角度观测到的棋盘格局$s’_k$，一直模拟到游戏结束
模拟结束以后根据胜负奖励r=1或者r=-1
将价值网络和结束以后观测的奖励结合

第四步: 回溯

每一次模拟都会得到一个价值记录下来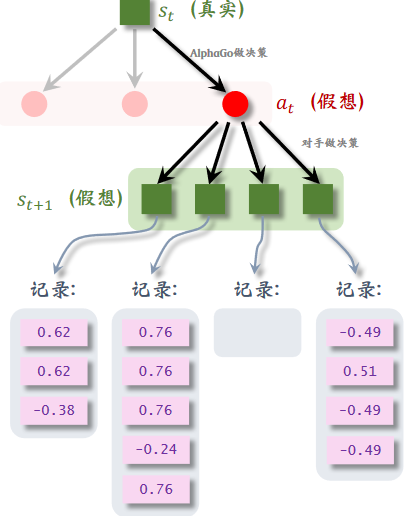
alt text
然后对与动作 $a_t$ 下的所有记录（图中是12条）求平均，得到价值 $Q(a_t)$ ，只要 $a_t$ 被选中一次就会更新 $Q(a_t)$

MCTS的决策

在做成千上万次模拟后
真正的决策就是

也就是在模拟中被选中的次数 $N(a)$ 最多的那个

而在状态 $s_{t+1}$ 的时候， $Q(a)$ , $N(a)$ 全部初始化为0，从头开始做模拟

训练策略网络和价值网络

AlphaGo2016版本的训练

1.先用模仿学习，行为克隆人类操作的方法进行训练策略网络
将 $\{(s_k,a_k)\}$ 二元组拿去训练策略网络 $\pi(a|s;\theta)$
策略网络输出的概率分布 $f_k$ 和数据集中以动作 $a_k$ 得到的one-hot编码 $\bar{a}_k$，将二者进行交叉熵处理，用随机梯度下降进行优化

2.之后用REINFORCE进一步训练策略网络，注意这个方法是针对玩一整局游戏得到的实际抽样
alt text
双方都是用策略网络，但只更新玩家的参数
游戏没结束的时候 $r_1=r_2=\ldots=r_{n-1}=0$
将游戏进行到最后，如果玩家赢或输，分别得到 $r_n=+1/-1$
这样每一步的预测 $u_1=u_2=\ldots=u_{n}=1/-1$
最后得到的公式如下:

3.训练价值网络
将训练好的策略网络做自我博弈，记录 $(s_k,u_k)$
让价值网络 $v(s_k;\omega)$接近 $V_{\pi}$，也就是 $u_k$
最后梯度下降解决