数学题推理论文合集
rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking
https://arxiv.org/pdf/2501.04519
核心点:
1.mcts生成的推理轨迹—-生成单步,代码生成验证
2.奖励模型训练—-利用mcts的Q值作为正确/错误的划分,而非reward label
3.自我迭代
Common 7B Language Models Already Possess Strong Math Capabilities
https://arxiv.org/pdf/2403.04706
使用合成数据
提出instability issue: 尽管模型在生成多个答案时具有较高的准确率,但难以保证在每次生成中都能稳定地产生正确答案
DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning
https://github.com/deepseek-ai/DeepSeek-R1/blob/main/DeepSeek_R1.pdf
关注点:
1.GRPO作为强化学习框架
2.语言一致性奖励—-虽然会降低模型性能,在R1-zero中使用正确性奖励和格式奖励(有没有把内容写在special token里面)
3.注意冷启动sft的格式,冷启动蒸馏的数据是long-cot(来源于deepseek-R1-zero),包含reflection,verification,格式检查的流程
4.第一轮RL收敛后,用rule-based rewards或者generative reward model(把ground-truth和模型预测扔给deepseek-v3),过滤掉mixed languages, long parapraphs, code blocks
5.收集完推理的600k和非推理的200k接下来做两轮sft,之后进行第二轮RL
总结rstar-Math, Deepseek-R1, kimi-1.5
参考文章:
https://mp.weixin.qq.com/s/DPdnhAH-c3uCR3UclVm4dA
The Lessons of Developing Process Reward Models in Mathematical Reasoning
https://arxiv.org/abs/2501.07301
之前的PRM用MC,用Best of N评估
基于MC的PRM问题: suboptimal performance of MC estimation,具体就是正确步骤答案不正确,不正确步骤答案正确,有大量噪声
Best of N评估问题: policy模型过程不对答案对,很大一部分最低分数集中在最终答案步骤上
PROCESSBENCH: Identifying Process Errors in Mathematical Reasoning
https://arxiv.org/pdf/2412.06559
7B Model and 8K Examples: Emerging Reasoning with Reinforcement Learning is Both Effective and Efficient
https://hkust-nlp.notion.site/simplerl-reason
code
使用PPO,而不是GRPO
qwen2.5-math-7B作为base,最开始token数降低因为base模型默认的输出模式是language+code
ruc
使用math, biology, physics, code, chemistry, puzzle的long cot数据
reward model未知
Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach
https://arxiv.org/pdf/2502.05171
code
latent space的另外一篇
模型架构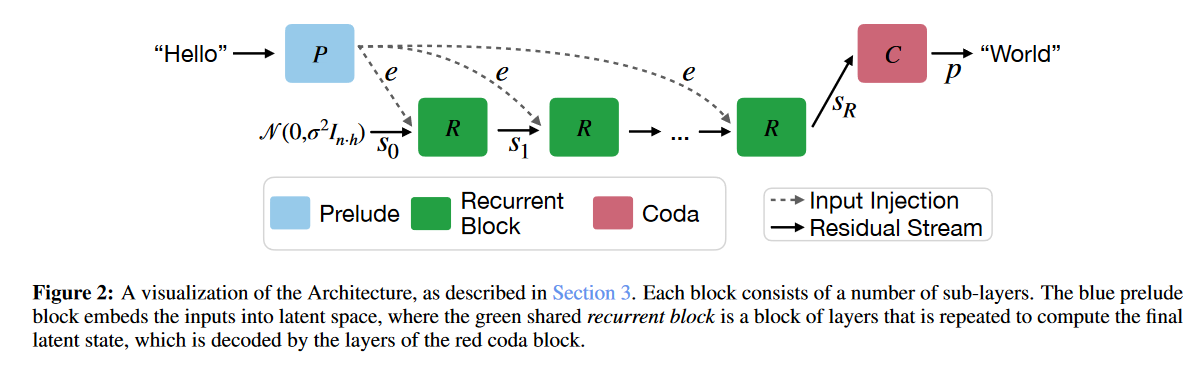
架构上由prelude, recurrent, coda三部分组成
注意图中e和s0,将上一层结果与当前token的embedding是用adapter矩阵融合(而非直接加法),2h->h
原因: 简单加法输入信息e可能在多轮递归计算中被逐渐削弱; 在每个递归步骤引入e可以稳定计算过程,并确保收敛结果与初始状态无关
使用随机分布初始化: 确保路径独立性,使得推理结果不依赖于初始值。避免梯度爆炸或消失,确保数值计算稳定。鼓励模型在推理过程中进行动态调整,而不是仅仅依赖记忆。使得模型在测试时泛化性更强。确保模型能在递归过程中进行更深入的计算,而不会陷入计算模式固化的问题。
模型递归深度r随机,采用log-normal Poisson distribution—-适应不同的计算预算,测试时可以直接使用不同的计算量,而不需要额外微调
截断反向传播,仅对最近的k=8次递归步骤进行梯度更新—-减少成本